What is the Difference Between Parabola And Hyperbola
A parabola and a hyperbola are both conic sections, which are shapes that result from the intersection of a plane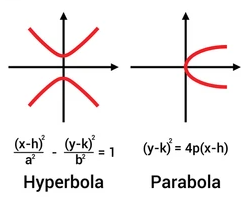
and a cone. However, they are different in their geometric properties and shape. A parabola is a symmetric and open-ended U-shaped curve that is defined by the set of all points that are equidistant from a fixed point, known as the focus, and a fixed line, known as the directrix. It can be used to represent the path of an object in motion under the influence of gravity. On the other hand, a hyperbola is a symmetric curve that is defined by the set of all points where the difference of the distances between two fixed points, called the foci, and any point on the curve is constant. Hyperbolas can be used to represent the path of an object in motion under constant acceleration.
parabolas have an eccentricity of 1, while hyperbolas have an eccentricity greater than 1. That means that a parabolic orbit looks more like a circle, while a hyperbolic orbit will look more like an ellipse. the circles and ellipses have closed curves while parabolas and hyperbolas have open curves.
Parabola vs Hyperbola – Comparison Table
Parabola | Hyperbola |
| It is a set of points in a plane that are equidistant from a straight line or directrix and focus. | It is the difference in distances between a set of points, which are present in a plane at two fixed points, it is a positive constant. |
| The Parabola has eccentricity e = 1 | The Hyperbola has eccentricity e> 1 |
| They always have the same shapes regardless of their shapes. | They can have different shapes. |
| Do not have asymptotes. | Have two asymptotes. |
| A parabola has a single focus and directrix | Parabolas have two focus points and also two guidelines. |
| There are two arms in a parabola that are essentially parallel to each other. | Not a single arm is parallel in a hyperbola. |
Explanation
while working on planetary motion, Kepler studied the orbits of planets as an ellipse. later on, Newton contributed his research and modified Kepler’s findings by saying that orbits actually are special conic sections e.g. parabola and hyperbola.
According to the research of Kepler and Newton, there are many similarities and differences between the parabola and the hyperbola. both geometric figures help to solve geometric problems concerned with conic sections.
let’s see how?
let’s cut a solid figure like a cone. we obtained a conic section as in the above picture. a section is a surface made on the surface of the solid figure with a plane. there are different figures that can be obtained such as circles, ellipsis, hyperbolas, and parabolas that are highly dependent on the angle of intersection between the axis of the plane and cone.
but,
we on this topic only have concerns with parabola and hyperbola. they have open curves while circles and ellipses have closed curves. the branches or arms of the parabola and hyperbola curves continue constantly until infinity.
when a cone is cut down at a right angle to its axis, a circular shape is obtained. if we cut the cone at less than a right angle, we obtain an ellipse. by cutting the cone parallel to the side of the cone, we get a parabola and the last one is when cutting the cone almost parallel to the axis to the side, we get the shape called a hyperbola.
What is Parabola?
when we divide a plane or flat surface into a conic shape, a parabola is formed. it is a surface parallel to the side of the cone and called the conic” section (curved, like a U-shape). on the other thing is important to remember that if we take any point from the parabola, the line from that point to the x-axis will always be equal to the focus or center point of the parabola.
both edges of the parabola curve will extend to infinity while their flat point can touch single, twice, or not a single time to the x-axis.
What is Hyperbola?
when we divide a cone into a conic section a hyperbola or conical section is formed which always remains parallel to its axis. it can be seen as two different identical branches with the same sizes and shapes like the English word “U”. both shapes are oriented in opposite sides or directions.
When are they formed?
the above two figures are formed when we graph a quadratic equation in which the variables are raised always in the second power of the square. it also remains on the second degree that does not go at a higher value than 2 like cubed or to any greater power.
when all the points in the quadratic equation are graphed at equidistance from its focal point, a hyperbola is formed. but if the points in the quadratic equation extend to positive constants it will result in a hyperbola.
to conclude:
parabola has one focus point. on the other hand, a hyperbola has two focus points that are mirror images of each other or places in opposite directions to each other.
What is Eccentricity?
we talked earlier in this article about the eccentricity of parabolas and hyperbolas. le’s known what is it.
it is the measurement of the deviation of any orbit of a shape. in other words, it measures how much a shape deviated from being a circle. a pure circle has an eccentricity equal to 0. if the circular shape deviates into an ellipse, the eccentricity will increase from 0 to a greater value.
the parabolic shapes have eccentricity always equal to 1 while hyperbolas have more than 1. look at our planet’s system. there is neither a parabola nor a hyperbola. they are almost similar to circular shapes.
Equations of Parabola and Hyperbola
- (y – k) squared = 4a (xh) is known as the equation of parabola where h is the x-axis, and k is the y-axis. a represents any real number except 0.
- ((x squared) / (squared)) – ((y squared) / (b squared)) = 1 is known as the equation of hyperbola where a and b are positive real numbers.
Conclusion
Hyperbola and Parabola Both the conic sections are different in size, shape, and other different criteria, including the formulas and equations. the major difference between hyperbola and parabola lies in the difference in eccentricity in both. parabola has eccentricity equal to 1 and has only one focus point while hyperbola has eccentricity greater than 1 and have two focus points mirrored to each other.
You May Also Like:
