Types of Angles
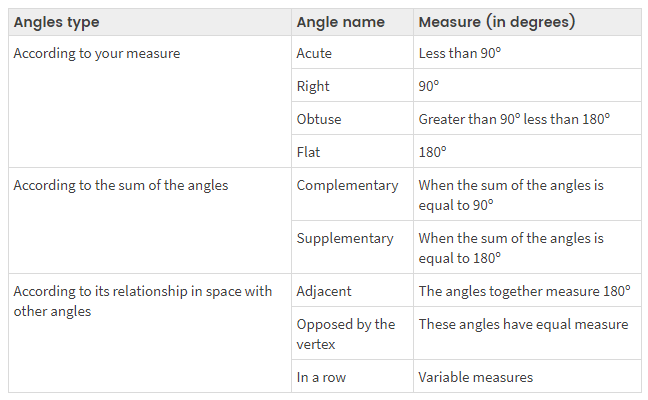
Angles are classified on the basis of three properties: based on their measure, sum, and position. however, Acute, Right, Obtuse, Flat, and Reflex angles are some common types of angles in Geometry.
What is an Angle?
An angle is a region of the plane between two rays with a common region called sides having a common origin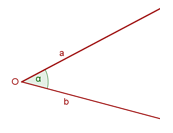
vertex. in other words, it is bounded by these two rays or sides starting from the same point known as the vertex. for example, the sum of the angles of a triangle is equal to 180º in total.
the angles are always formed by intersecting two lines with each other. both lines will also coincide from the same vertex to the rest of the sides or points. these angles also have amplitude in degrees that can be measured with the help of a protector.
Types of Angles – A Comparative Chart
Types of Angles According to their Measurement
this type of angle measurement refers to simple angles and is a measurement of the opening between two sides of the angle and is always expressed in degrees (º). the degree (º) measurement is also known as sexagesimal degree º which is the amplitude of the angle resulting from dividing the circumference into 360 equal parts.
Radian:
“The Radian (rad) is used when we measure the central angle of a circle whose arc length coincides with the length of its radius.”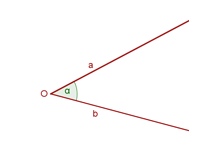 
1Rad= 57° 17′44.8″
360°= 2πRad
The classification of the angles according to their measure would be:
Acute angles
if the amplitude of an angle is less than 90º (> 90º) it is known as the acute angle. so, all those angles having amplitude fewer than 90º are acute angles. when somebody tries to separate the two adjacent fingers, an acute angle is formed. another way to elaborate on an acute angle is that the angle having inclination is greater than 0 ° and less than 90 °, not including the latter measure. is known as acute. an ice cream cone is a good example of that.
Right angles
if the angle measures exactly 90º, it is known as a right angle. all those angles that measure exactly 90º are right angles. the angles of the square and rectangle are right and measure exactly 90º. the amplitude of the right angle also measures 90° and starts from the vertex having perpendicular sides.
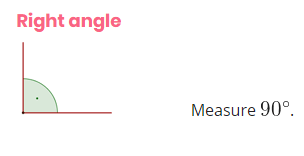
Obtuse angles
all the angles measure more than 90º and less than 180º (> 90º and <180º) are obtuse angles. we can also is defined the angles that measure between 90º and 180º. the opening of the wings of some airplanes and the opening of a fan is a good example of such type of angle. they have an amplitude greater than 90 ° and less than 180 °, not including the aforementioned measurements.
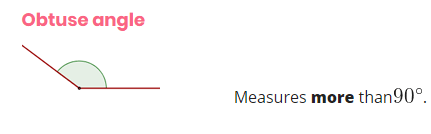
Flat or Plan angles
flat or plan angles are measured exactly 180º. they also measure 180º and looks like a straight line. a straight angle is formed by joining two right angles. they also have an amplitude measure of 180 °. This angle has a particular characteristic, and that is that its two lines join from the vertex forming an extension in the form of a straight line. For example, when the hands of the clock show 03:45 minutes. In this case, the small hand marks the number three and the large hand marks the number 9. Another example may be when the clock marks 12:30 with its hands, among others.
Concave angles
They are the angles whose amplitude is greater than 180º and less than 360º (> 180º and> 360º). The concave angle is one whose amplitude measures more than 180 °, but less than 360 °. For example, if you have a round cake cut into parts from its center point, but less than half of it has been eaten. The remainder of the paste forms a concave angle.
Convex angles
They are the angles that measure between 0º and 180º (> 0º and> 180º)
Full angles
A complete angle is one that measures, exactly 360º. It looks like a circumference. It is the one that measures 360 °, in this sense, the line that starts it returns to its point of origin. For example, go around the world and finish in the same starting position.
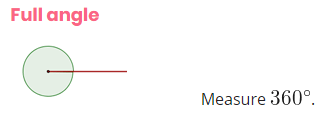
Null angle
Measure 0°. The rays that form the angles coincide.
Negative angle
Measures less than 0°. The negative angles rotate in the clockwise direction, ie, in the sense that the clockwise move. A negative angle can be converted into a positive angle by adding 360°.
An angle greater than 360 °
It measures more than one lap. An angle of 390° = 360° +30°, if we represent it, it coincides with an angle of 30°. An angle of 750° = 2.360°+30°, if we represent it, it coincides with an angle of 30°. If we want to pass an angle to the first turn, we divide the angle by 360 °: The quotient is the number of turns it makes, and the rest is the resulting angle that corresponds to the first turn.
Types of angles with respect to their sum
When we have two angles, we can classify them as:
- Complementary angles: are those whose sum is equal to 90º. For example, the complementary angle of a 30º angle is another of 60º (30º + 60º = 90º).
- Supplementary angles: are those whose sum is equal to 180º. For example, the supplementary angle of a 30º angle is another 150º (30º + 150º = 180º).
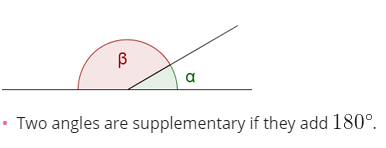
Types of Angles According to their position
This difference takes into account the position of one angle with respect to another (s).
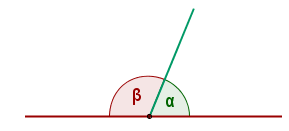
Adjacent angles:
The angles are adjacent when one of the sides is shared and the other sides form a straight line (equal to 180º). they are part of the related angles. These have a common vertex and side, but the other sides are made up of opposite rays. The sum of these angles adds up to 180 ° of amplitude.
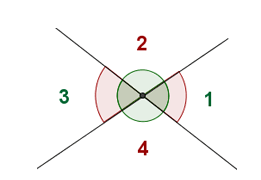
Opposite angles by the vertex:
They have the same vertex while the sides are extensions of each other. We can get opposite angles to the vertex when we open scissors. they are angles that are opposed from the vertex and whose sides are formed by the rays that are opposite of the sides of each angle.
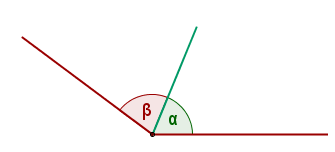
Consecutive angles:
Consecutive angles are those angles that share aside, regardless of their measure or the sum of the two angles. When consecutive angles are formed on one side of a line they add up to 180º. When the angles are consecutive around a point, they add up to 360º. For example, the rudder of a ship has consecutive angles. are those that have the same vertex and side in common. That is, it is at an angle right next to each other.
Angles between parallels and a transverse line
Corresponding angles:
The angles 1 Y 2 are equal.
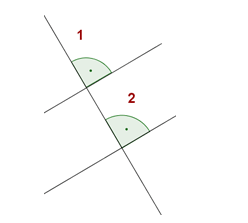
Alternate internal angles:
The angles 2 Y 3 are equal.
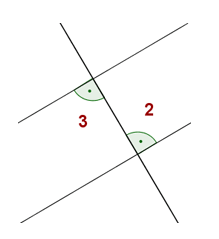
Alternate Exterior Angles:
The angles 1 Y 4 are equal.
Angles on the circumference
Central angle:
The central angle has its vertex in the center of the circumference and its sides are two radii. The measure of an arc is that of its corresponding central angle.
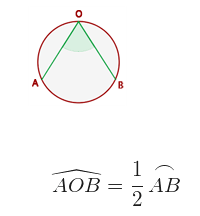
Inscribed angle:
The inscribed angle has its vertex on the circumference and its sides are secant to it. Measure the half of the arch that it covers.
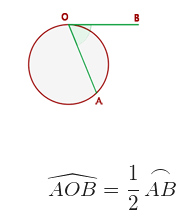
Semi-inscribed angle:
The semi-inscribed angle vertex is on the circumference, one side secant and the other tangent to it. Measure the half of the arch that it covers.
Inner angle:
Its vertex is inside the circumference and its sides secant to it. Measure half of the sum of the measurements of the arches that cover its sides and the extensions of its sides.
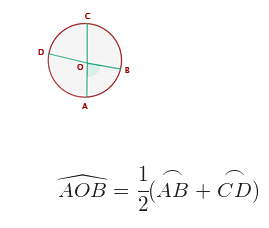
Outside angle:
Its vertex is a point outside the circumference and the sides of its angles are either secant to it, or one tangent and another secant, or tangent to it. Measure half the difference between the measurements of the arches that span their sides on the circumference.
Angles of a regular polygon
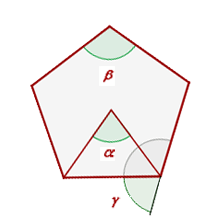
The central angle of a regular polygon:
It is the one formed by two consecutive radii.
Example
Yes, n is the number of sides of a polygon:
Central angle = = 360° ÷ n
Central angle of regular pentagon = 360° ÷ 5 = 72°
Interior angle of a regular polygon:
It is formed by two consecutive sides.
Inner angle = 180° – Central angle
Interior angle of regular pentagon = 180° -72° = 108°
The exterior angle of a regular polygon:
It is the one formed by one side and the extension of a consecutive side.
The exterior and interior angles are supplementary, that is, they add 180°.
Outside angle = Center angle
An exterior angle of a regular pentagon = 72°
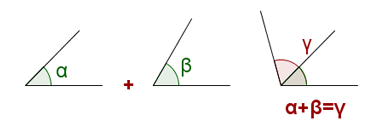
Sum of two angles
The sum of two angles is another angle whose amplitude is the sum of the amplitudes of the two initial angles.
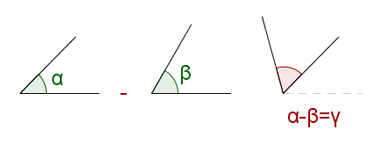
Subtraction of Two Angles
The subtraction of two angles is another angle whose amplitude is the difference between the amplitude of the greater angle and that of the smaller angle.
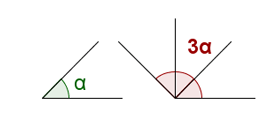
Multiplication of a number by an angle
The multiplication of a number by an angle is another angle whose amplitude is the sum of as many angles equal to the given one as indicated by the number.
Division of an angle by a number
Dividing an angle by a number is finding another angle such that multiplied by that number gives the original angle.
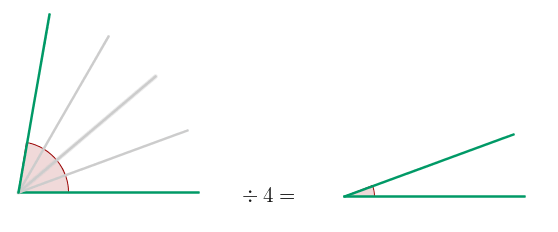
You May Also Like:
