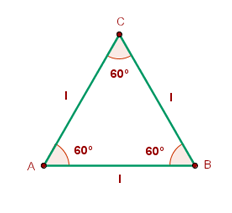
Equilateral Triangle
Triangles are closed figures joining with straight line segments .there are different types of triangles from which the Equilateral Triangle is a regular polygon figure that has three equal-length congruent sides (same measure). hence all three angles should also be equal (equiangular). as the internal angles are acute, the equilateral triangle is itself acute.
since, we knew that all the sides and angles are equal in length, their sum will also be equal to 180º and each interior angle will be 60º.
What are the Elements of the Equilateral Triangle?
- for equilateral triangle, sides a = b = c.
- ∝ = β = γ = 60º
- x=y=z= 120º or obtuse (greater than 90º)
Equilateral Triangle Area
The area of a flat figure like the Equilateral Triangle represents the size of its surface. the multiplication of base (b) with height (h) and dividing by 2 will give us the area of an equilateral triangle. in other words, the area will be one-half of the base (a) times its height.
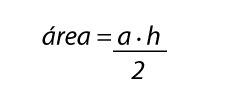
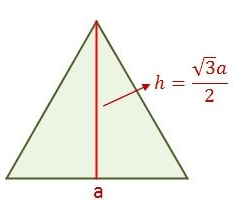
let’s suppose we have a height √of 3a/2. by putting the value of height from the above figure we have the area of an equilateral triangle:
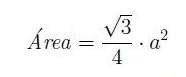
The perimeter of an equilateral triangle
as the following triangle has three sides all equal to each other, the perimeter corresponds to the sum of all sides or three times the length of one of its sides ( a ).
Mathematically,
P = a + a + a = 3a
equilateral triangle height
to find the height of an equilateral triangle we use the Pythagorean theorem. for this purpose, let us divide the triangle into two parts to make a right triangle. now take the sides a, a / 2, and height h. where sides a / 2 and h are known as legs while a is called the hypotenuse.
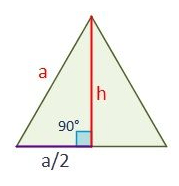

What is the Pythagorean theorem?
this theorem states that two legs of the right triangle lie on the hypotenuse. the two sides that are characteristic a right triangle are known as the legs while the longest opposite side to the legs is the hypotenuse.
according to the theorem:
the square of the hypotenuse is equal to the sum of the square of its legs.
c² = a² + b²
where a and b are two legs and c points to the hypotenuse.
Properties
The following properties fall under the Mentioned triangle:
- Angle Bisector:
- Segment Bisector:
- median is that line that starts from mid of its any side and meets at the vertex of another opposite side. this means, we can draw three medians at a time and they will meet at a single point called the center of gravity.
- axes of symmetry: it has three axes of symmetry that pass through the midpoint of each opposite side and its vertex
- consists of three equal sides
- known as a regular polygon having three sides.
- The area is equal to √3a2/ 4
- The perimeter is equal to 3a.
- all the angles are 60º and are congruent with each other.
- centroid and ortho-center meet at the same point.
Questions and Solved Excercise
FAQs (Frequently Asked Questions)
What is the equilateral triangle?
Ans: it is a regular polygon triangle that has three sides of equal lengths as well as equal angles. the internal angles are called congruent and are 60º each.
What is an equilateral triangle example?
Ans: rack in billiards, a slice of a pizza is an example of such type of triangle.
What is the area and perimeter of an equilateral triangle?
Ans: the area is said to e √3 a2/ 4 while the perimeter is equal to 3a. where a is the side of an equilateral triangle.
What are the rules for an equilateral triangle?
Ans: basic properties and rules are given below:
- it is a regular polygon in geometry.
- All three sides are equal in length.
- All three angles are congruent and equal to 60º.
- The ortho-center and centroid meet at the same point.
What are the 3 main types of triangles?
Ans: equilateral, isosceles, and scalene are three major types of triangles based on their sides.
How many sides does an equilateral triangle have?
Ans: it has 3 sides all equal in length.
You May Also Like: