what is the Difference Between Rhombus And Parallelogram?
A rhombus and a parallelogram are both quadrilaterals, which are shapes with four sides and four angles, but they have some key differences.
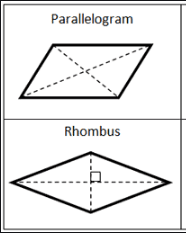
A rhombus is a quadrilateral with all sides of equal length, and opposite angles are congruent. It can also be defined as a parallelogram with all sides congruent. A rhombus also has opposite sides parallel and opposite angles equal. The diagonals of a rhombus bisect each other at right angles.
A parallelogram, on the other hand, is a quadrilateral with opposite sides parallel. The opposite angles are also congruent. A parallelogram can have sides of different lengths and the diagonals do not bisect each other at right angles.
In this article, you are going to learn a complete explanation of the Difference Between Rhombus And Parallelogram in detail.
This Article Also includes:
- Overview
- What is Rhombus?
- What is Parallelogram?
- Examples of both
- Lots more…!
So if you want to get benefits from this post you’ll love this article.
Let’s Dive right in…!
Overview
in mathematical geometry, we have different types of quadrilaterals. a quadrilateral is a polygon having four sides. parallelogram, kite, square, rhombus, rectangle, and trapezium are common types of quadrilaterals. they all possess almost similar characteristics but are known as different from each other.
people often seem to be confused regarding Parallelograms and Rhombi. they might think that both are the same in pictorial view and only named interchangeably.
but…!
although both Rhombi and Parallelograms look similar and both have four sides and vertices, they are completely different shapes.
Rhombus vs Parallelogram in Tabular Form
| Rhombus | Parallelogram |
|---|---|
| All sides are of equal length | Opposite sides are parallel |
| Opposite angles are congruent | Opposite angles are congruent |
| Opposite sides are parallel | Opposite sides are equal in length |
| Diagonals bisect each other at 90 degrees | Diagonals bisect each other at 180 degrees |
| The area can be calculated using d1*d2/2 | The area can be calculated using b*h |
| All angles are 90 degrees | Opposite angles are congruent |
| It is a special case of a parallelogram | It is a more general case |
| Rhombus is a square when all the angles are 90 degrees | A parallelogram is a rectangle when all the angles are 90 degrees |
| The diagonals of a rhombus bisect each other | The diagonals of a parallelogram do not bisect each other |
| It is a plane figure | It is also a plane figure |
What is a Rhombus?
The word “rhombus” is Derived from the Greek ῥόμβος (rhombos), having meant something which can spin which derives from the verb ῥέμβω (rhembō), meaning “to turn round and round. in Euclidean geometry, a rhombus four-sided equal lengths flat-shaped quadrilateral which also known as an equilateral quadrilateral.
their opposite sides are always congruent and parallel to each other. a diamond is a suitable example of a rhombus. it is a similar or special form of kite shape which do not self-intersect.
A rhombus has an equal measure of its opposite angles. moreover, if two of their diagonals will perpendicular to each other, it is called an orthodiagonal rhombus. each type of rhombus is considered a parallelogram but not every parallelogram is considered a rhombus.
What is Parallelogram?
A parallelogram is a simple, flat-shaped, and non-self-intersecting quadrilateral. it has two pairs of parallel and congruent sides with equal lengths. their opposite angles are also equal in measure. the diagonals bisect each other in a way that they form congruent triangles with each other.
Conclusion
In summary, the main difference between a rhombus and a parallelogram is that a rhombus has all sides congruent and diagonals bisect each other at right angles, while a parallelogram has opposite sides parallel and opposite angles congruent and diagonals don’t bisect each other at right angles.
Other Similar Questions to Rhombus And Parallelogram:
- difference between rhombus and square
- what shape is a parallelogram but not a rhombus?
- a parallelogram is a rhombus always, sometimes, or never?
- parallelogram vs rhombus vs trapezium?
- is a rhombus always a parallelogram?
- difference between parallelogram and trapezium
- difference between rectangle and parallelogram
- is a rectangle a parallelogram?
