Difference between Area and Perimeter
In this article, you are going to learn a complete explanation of the difference between Area and Perimeter.
This Article Also includes:
- What is the area?
- What is the perimeter?
- Examples of both
- Lots more…!
So if you want to get benefits from this post you’ll love this post.
Let’s Dive right in…!
Area and perimeter are two important concepts in geometry that are often used in measuring the size and shape of different objects.
The area is a measure of the amount of space inside a closed shape, such as a rectangle or a circle. It is typically measured in square units, such as square feet or square meters. The formula for finding the area of a shape depends on the shape in question. For example, the area of a rectangle is found by multiplying the length of the rectangle by its width, while the area of a circle is found by multiplying pi (π) by the square of the radius.
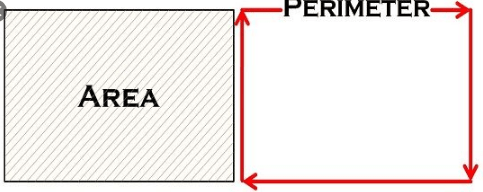
Perimeter, on the other hand, is a measure of the distance around the outside of a shape. It is also called the “length of the boundary.” It is typically measured in linear units, such as feet or meters. The formula for finding the perimeter of a shape also depends on the shape in question. For example, the perimeter of a rectangle is found by adding up the lengths of all four sides, while the perimeter of a circle is found by multiplying pi (π) by twice the radius.
To put it simply, area measures the space inside a shape, while perimeter measures the length of the shape’s boundary. They are both important measurements for different applications, such as calculating the amount of paint or carpet needed to cover a room or determining the length of fencing needed to enclose a field.
in a nutshell, the basic difference between Area and Perimeter is that Area is the measurement of space inside a shape or the number of square units inside a shape or object while Perimeter is the measurement of the distance around the shape. the area can be calculated by the formula A= L x W (length x width) and the perimeter is measured through the formula P= L x L x W x W ( Length x Length x Width x Width).
Difference between area and perimeter in Tabular form
Area | Perimeter |
Definitions | |
| The region or space inside of a closed shape is known as the area. | The distance outside or around a closed shape is called its perimeter. |
Examples | |
| For example, the inside area of a cricket playground for a player to hit a boundary. | Putting the fence on the border of a country.
|
Measurement units | |
| The base unit is (sq) e.g 48ft², 68in². | It is measured in simple dimensions e.g 500m. |
Area and perimeter of a rectangle | |
| As a rectangle, LW is length and width. | As a rectangle, we take 2L+2W where L and W stand for Length and Width. |
What is Area?
the area is a quantity that can be defined as the region of space surrounded by a 2D object. the SI unit for area is a square meter or m². in mathematics we deal with many geometric shapes to find their areas such as ellipses, circles, triangles, rectangles, and so on. for example, we want to calculate the area of a polygon. we divide the polygon into many possible triangles to do so.
we have to deal with various types of area formulas for different shapes e.g., circles, triangles, rectangles, etc., and sometimes we need to convert one type of figure to another to find the area. for example, we divide the polygon into various triangles around the curved path to calculate its area.
these are simple shapes with a fixed size. on the other hand, dealing with solid shapes like cylinders, cones, or spheres, we calculate their boundaries as area. now we suppose to calculate their surface area than that of the area.
Units of the Area while Measuring
we use several units of lengths in calculus and geometry and each unit has its own corresponding unit of area. for example, the area of a square with its side lengths can be measured with m², cm², mm²,km²,ft², yd,², etc. depending on the unit lengths, we are measuring this area. however, the derived SI unit of area is m².
What is Perimeter?
the word perimeter is derived from the Greek περίμετρος perimetos from περί peri “around” and μέτρον metron “measure”. It is a distance, outer boundary, or path around a two-dimensional shape. for a circle or ellipse, it is known as the circumference.
as discussed above, it can be the fence around an orchard or the boundary of a playground. the circumference means how far the shape can be rolled in one rotation.
Formulas related to Perimeter
Shape | Formula |
| Triangle | a+b+c |
| Circle | 2πr = 2πd/2=πd |
| rectangle | 2(l+w) |
| square or rhombus | 4a |
| regular polygon | 2nbsin(π/n) |
| equilateral polygon | n X a |
| general polygon | a1+a2+a3+a4……..+an=(∑¹ai) |
You May Also Like: