Limit Calculus Formula and Methods to solve determinate and indeterminate problems

The concept of limit usually shows the closeness. The two major operations in math derivatives and integral from calculus both depend on the theory of limits. Limit is a value that a variable quantity from which you can approaches as closely you desires.

The theory of limit is that in any two real number there is always another one in place you can say there are infinitely many more real numbers between two real numbers.

Moreover, in this article, basic idea of function and different methods to evaluate the limit are discussed with the help of examples.

Formula of limit

The limit of a function is basically written as

Lim _{x→ c} f(x) = L

And read as “the limit “f of x” as “x” approaches “c” equals to L”.

f(x) → L as x → c,

which reads “f of x tends to L as x tends to c”.

Continuous Function and Discontinuous Function

Continuous function

To check function is continuous if three basic conditions are fulfilled then it is a continuous function

• If function g(b) exists.
• Lim _{y→ b} g(y) exists.
• Lim _{y→ b} g(y) = g(b)

Discontinuous function

If any one of these conditions does not hold then it is discontinuous.

Different Ways to Calculate Limits.

In this section, we will discuss the different methods which help to evaluate limits. Each method will explain with the help of some examples. Moreover, according to the situation of a problem, we will use a suitable method to get their answers. A few methods are discussed below to find limits.

1) Direct Substitution method

2) Factorization

3) Rationalization

4) L’ Hospital Rule

1) Direct Substitution Method

If we have a continuous function then we can easily find its limit by using the direct substitution method. Here are a few examples of polynomial functions you can easily calculate their limits by using the direct substitution method

For Example:

Lim _{x→ 1} (x³+2)

Solution:

Applying limit

= Lim _{x → 1} x³ + Lim _{x→ 1} 2

= (1)³ + 2

=1+2

= 3

For Example:

Lim _{x→ 1} (x²+5x+3) / (x+4)

Solution:

Applying limit

= (1²+5(1) +3) / (1+4)

= (1+5+3) /5

=9/5

Factorization method

Initially, we discuss the basic need of its use we saw an example if we put limit, it becomes Indeterminate form so it helps to make factors and then cancel the like terms to make it determinate form.

Example 1:

Lim _{y → 1} (y³-1)/(y-1)

Solution:

It is making 0/0 form which is the indeterminate form

To get its answer before putting limit we will make factors and cancel the like term

In algebraic formulas we know (y³-1) = (y-1) (y²+y+1) now replacing it in original function it becomes

Lim _{y → 1} (y-1) (y²+y+1) / (y-1)

Now after cutting the like terms, it becomes

Lim _{y → 1} (y²+y+1)

Now put limits to get the answer by applying the limit

= (1²+1+1)

= (1+1+1)

=3

Here are a few more relevant problems to evaluate with the help of factorizing method.

Example 2:

Lim _{y → 2} (y²-3y+2)/ (y²-4)

Solution:

Lim _{y → 2} (y-1) (y-2) / (y-2) (y+2)

canceling the liking terms

= Lim _{y → 2} (y-1)/ (y+2)

Putting the limits

= (2-1)/2+2

=1/4

Similarly, Lim _{y → 1} (y⁴-3y+2)/(y⁵-4y+3) can be solved by this technique.

Rationalization

Now the basic need for rationalization is the same as factorizing to make an indeterminate form into a determinate form. From examples, you can easily understand the basic need to rationalize the problem.

For Example:

Lim _{y → – 2} (y + 2) / (y +4) – 2

Solution:

It is 0 / 0 form if we put limit rationalizing it to make it in determinate form

=   Lim _{y → – 2} (y + 2) / (y +4) – 2 * (y +4) + 2 / (y +4) + 2

= Lim _{y → – 2} (y + 2) (y +4) + 2 / (y +4) – 2

= Lim _{y → – 2} (y + 2) (y +4) + 2 / (y + 2)

Canceling the like terms

= Lim _{y → – 2}   (y +4) + 2

It is now in the determinate form now put the limits to get the answer

= (-2 +4) + 2

= 2 + 2

= 2 2

Similarly, there are many problems like this that can solve by this rationalization method.

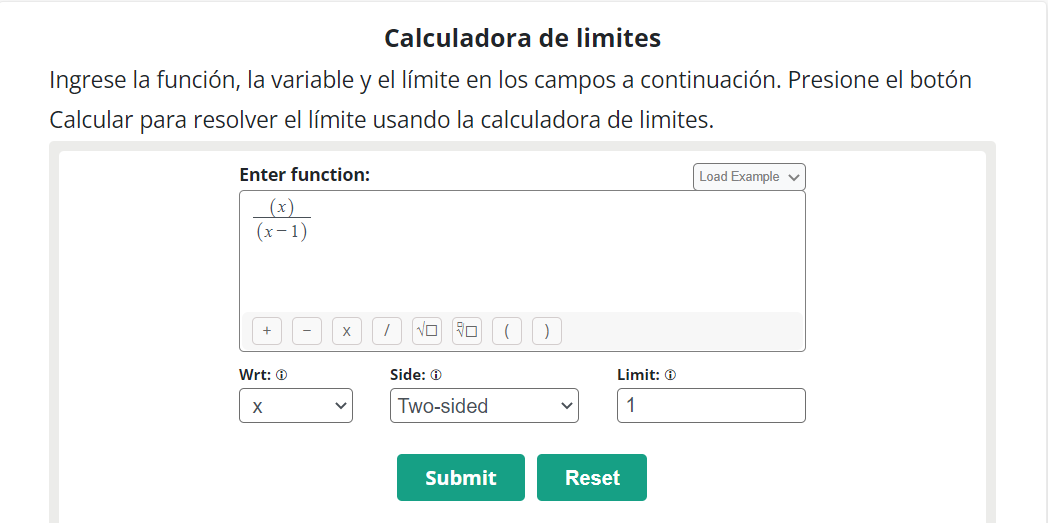
Try a limit calculator by Allmath to evaluate the problems of limit calculus through the above methods to get rid of the above lengthy calculations.

L ‘Hospital rule

This technique deals with trigonometric functions also and it is also used to make the function in determinate form by differentiating the numerator and denominator until it is giving definite answer after putting limits. With the help of examples, it will be cleared fully.

For Example:

Lim _{x → 0} Sin(x)/x

Solution:

Which is 0/0 form

Now using L’ Hospital Rule

Taking the derivative of the numerator and denominator

After taking a one-time derivative it becomes

= Lim _{x → 0} cos(x)/1

Now it is not 0/0 form

Putting limits

= cos (0)/1

= 1/1 =1

For Example:

Lim _{x → 0} (3x⁴-6x³+5x²+8x) / sin(x)

Solution:

It is also an indeterminate form

Now using L’ Hospital Rule

Taking the derivative of the numerator and denominator

After taking a one-time derivative it becomes

= Lim _{x → 0} (12x³-18x²+10x+8) / cos(x)

Now it is determinate form put the limit to get the answer

= Lim _{x → 0} 12x³– Lim _{x → 0} 18x²+ Lim _{x → 0} 10x+ Lim _{x → 0} 8)/ Lim _{x → 0} cos(x)

= 12(0)³-18(0)²+10(0) +8 / cos (0)

= 8 / 1

= 8

Summary

In this article, basic idea of limit discussed in starting after its methods to evaluate the limits also with the help of examples. Limits are evaluated concept of continuous function and discontinuous function and methods for indeterminate form and determinate form also discussed in this article. After reading and understanding this article anyone can easily defend this topic.