Concept of Limit in Calculus

Calculus defines the limits as the point at which a function approaches the output for the specified input values. Let’s say that we go in-depth on the definition and symbol of the purpose’s boundaries as well as its applications and models.

In mathematical model based on the clue of understanding, is used primarily to allocate values to certain purposes at points where no values are well-defined, in such a way as to be dependable with neighboring values.

Limits are the technique by which the derivative or rate of change of a function is calculated and they are used all over analysis as a method of making approximations into particular amounts, as when the capacity inside a curved state is well-defined to be the limit of approximations by rectangles.

In this article, we will discuss the basic definition, formula, properties, and application of limit.

Definition of limit

A limit is a value that a function or sequence approaches a certain value, approaches infinity or negative infinity. More formally, a limit is defined as follows:

Suppose g is a function defined on some interval containing a point a, except possibly at a self. We say that the limit f as x approaches a is L, denoted by

Lim_x→a g(t) = L

If for every ϵ > 0, there exists a δ > 0 such that if 0 <|f(x)-L|< ϵ.

This definition means that as x is closer to a, g(t) gets arbitrarily close to L. The value of L is a limit that exists, it may be not equal to the toe value of the function. Two different limitations may be approached by a function.

One where the adaptable approaches its limit over values greater than the limit and the other where the adjustable approaches its limit through values minor than the limit. Although the boundary, in this case, is not precisely defined, it still has a right and left boundary.

Basic Laws of Limits

Consider f(x) and g(x) can be described for all “x ≠ a” over an open interval accommodate. Suppose that S and T are real numbers, such that,

Lim_x→a f(x) = S

And

Lim_x→a g(x) = T

Let “a” be a constant. The important laws of limits are:

1.     Sum law of limits:

Lim_x→a [f(x) + g(x) ] = Lim_x→a f(x) + Lim_x→a g(x) = S + T

2.     Difference law of limits:

Lim_x→a [f(x) – g(x)] = Lim_x→a f(x) – Lim_x→a g(x) = S – T

3.     Constant multiple law:

Lim_x→a [c. f(x)] = c. Lim_x→a f(x) = cS

4.     Product law of limits:

Lim_x→a [f(x) * g(x)] = Lim_x→a f(x) * Lim_x→a g(x) = S * T

5.     Quotient law of limits:

Lim_x→a [f(x)/g(x)] = Lim_x→a f(x) / Lim_x→a g(x) = S / T. Where M ≠ 0.

6.     Power law of limits:

Lim_x→a [f(x)]ⁿ  = [Lim_x→a f(x) ]ⁿ = Sⁿ . For positive integer n.

Applications of limits in daily life

Every time a steady-state solution is applied in the real world, real-life applications of limits are used.

• As an illustration, we might start a chemical reaction in a beaker with two chemicals, which eventually transforms into a new substance. As the time approaches infinity, the limit of a function is the quantity of the newly formed compound.
• The temperature ultimately approaches the room temperature where the glass is stored if you place an ice cube in a glass of warm water and monitor the temperature over time. As the time nears infinity, measuring the temperature once more becomes a limit.
• Limits have a wide variety of uses in various areas of mathematics besides just finding derivatives and integrals in calculus .some examples such as
• Measuring the magnetic, electric, and other fields’ amplitudes is useful.
• From the huge, complex functions, the most pertinent information is extracted using limits.

Example Section:

Example 1

Evaluate the limit of (5x⁵ – 3x³ + 6x² – 3x + 3) at x = 5.

Solution

Step 1:

We write the given function

lim_x→5 (5x⁵ – 3x³ + 6x² – 3x + 3)

Step 2:

We apply the limit on the given function

= lim_x→5 (5x⁵) – lim_x→5 (3x³) + lim_x→5 (6x²) – lim_x→5 (3x) + lim_x→5 (3)

Step 3:

Now apply the limit on the variable and the constant start of the limit.

= 5 lim_x→5 (x⁵) –  3 lim_x→5 (x³) + 6 lim_x→5 (x²) – 3 lim_x→5 (x) + lim_x→5 (3)

Step 4:

To Simplify the value.

= 5(5)⁵ – 3(5)³ + 6(5)² – 3(5) + 3

=  5 x 3125 – 3 x 125 + 6 x 25 – 15 + 3

= 15625 – 375 + 150 – 15 + 3

= 15778 – 390

= 15388

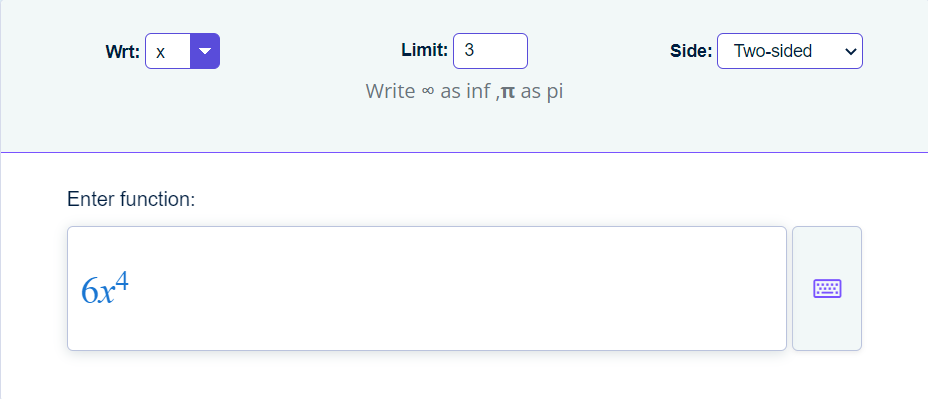
Example 2

To compute the limit of the function lim_x→3(6x⁴).

Solution

Step 1:

Now, we write the given function.

lim_x→3(6x⁴)= lim_x→3 (6x⁴)

Step 2:

Apply the limits on the function.

lim_x→3(6x⁴)= 6 lim_x→3 (x⁴)

Step 3:

We use the value of x.

lim_x→3(6x⁴)= 6 (3)⁴

Step 4:

Rearranging the value.

lim_x→3(6x⁴)= 6 x 81

lim_x→3(6x⁴)= 486

Try a limit solver to cross-check the result and evaluate more limits problems with steps in a fraction of a second.

Example 3

Evaluate lim_x→1(5x²/x+3).

Solution

Step 1:

Write the given function.

lim_x→1(5x²/x+3).

Step 2:

Now we apply the limit of a given function

lim_x→1(5x²/x+3) = lim_x→1(5x²)/ lim_x→3(x+3)

step 3:

Rearranging the limits

lim_x→3(5x²/x+3) = 5 lim_x→1 (x²)/ lim_x→1 (x)+ lim_x→1 (3)

Step 3:

Putting the value of x.

lim_x→1(5x²/x+3) = 5(1)²/ (1+3)

lim_x→1(5x²/x+3) = 5/4

Summary

In this article, we’ve discussed the basic definition of limits, the formula of limits, the applications of limits in daily life, and the laws of limits. Additionally, with the help of examples explained the topic in detail. Now, you can completely understand this article, anyone can easily solve any problem related to the limits.