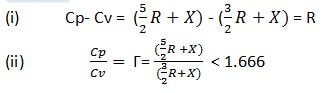Heat Capacities of Gases: (at constant volume and Temperature)
[wp_ad_camp_1]
Matter exists due to the possession of energy and there is a close interaction between energy and matter. the matter has the capability to retain to a greater or lesser extent a certain amount of energies.
in this article, we have to look at the capabilities of the gasses to absorb various amounts of energies by the change of temperature.
the heat capacity of the gas is the amount of heat required to rais the temperature of the gas by 1°C (1 k). if the quantity of the substance is one gm, then it is called specific heat.
if the weight of the gas is one gram, then it is called specific heat.
heat capacities are denoted by C. the rise of temperature is noted from 14.5° to 15.5°C. it is measured in calories K-1mol-1 in non-SI units.
what is heat capacity formula?
you can calculate heat capacity with the following formula:
Q=mcΔT
Heat capacity = mass x change in temperature x specific heat
Where Q = heat capacity ( in Jouls)
m = mass ( in grams)
c = specific heat of the object ( in °C)
ΔT = change in temperature ( °C)
[wp_ad_camp_2]
The Units of Heat capacity :
in SI units the molar heat capacity is expressed as JK-1mol-1.
Types of Heat Capacities
- Heat Capacity at constant volume (Cv)
- Heat capacity at constant pressure (Cp)
let us try to understand the first one,
Heat capacity at constant pressure (Cp)
it is the amount of heat which is required to raise the temperature of one mole of gas by 1°C, when the volume is kept constant and the pressure is allowed to increase.
we are going to discuss only monoatomic gases at the moment. monoatomic gases have the only translational motion and the kinetic energy possessed by one mole of monoatomic gas is given by ![]() let us increase the temperature of this monoatomic ideal gas by 1°C. temperature change is from T to (T+1). and its kinetic energy K` at ( T+1) °C, is
let us increase the temperature of this monoatomic ideal gas by 1°C. temperature change is from T to (T+1). and its kinetic energy K` at ( T+1) °C, is ![]() Subtraction Equation (1) from (2)
Subtraction Equation (1) from (2)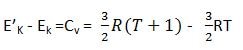
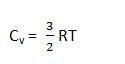
Since R= 8.3193 JK-1 mol-1
[wp_ad_camp_3]
it means that if we have one mole of any monoatomic gas, then molecules will absorb the same amount of heat i.e., 3/2R, when their temperatures are increased by one kelvin.
useful information!
the monoatomic gas like He, Ne, Ar and vapors of Hg, K and other metals have Cv value of 12.48Jk-1 mol-1.
the reason is that the one mole of all the monoatomic elements have Avogadro’s number of atoms, in other words, 12.48 jouls is the demand of Avogadro’s number of atoms, when we change their temperature by 1°C (1 °K) say for He, Ne, Ar etc.
now you understand the first property of heat capacity. we try to understand the second,
Heat capacity at constant pressure (Cp)
it is the amount of heat required to raise the temperature of one mole of gas by 1°C (1K) keeping the pressure constant and the volume is allowed to increase.
it is denoted by Cp.
[wp_ad_camp_4]
Actually,
When we measure Cp value of gas then some energy is expended in the expansion of the gas and pressure-volume work is done. let us calculate the additional pressure-volume work.
the general gas equation for one mole of an ideal gas is
PV = RT ……. (4)
suppose that by increasing the temperature by one kelvin from T to ( T+1). the volume changes from V to (V + ΔV), so
P( V+ ΔV) = R( T+1) …… (5)
PV+ PΔV = RT+R …….. (6)
substitution equation (4) in equation (6).
RT + PΔV = RT + R
so, PΔV = R …….. (7)
[wp_ad_camp_5]
It means that R is the contribution to the molar heat capacity due to the external work. it means that the value of the Cp should be as follows:
substituting the value of the general gas constant R, as 8.3143Jk-1 mol-1.
it means that for monoatomic ideal gases, the amount of heat required to raise the temperature by one kelvin for one mole along with the increase of volume so that pressure remains the same is 20.8 J.
Important conclusions for Cp and Cv:
from the expressions of Cp and Cv , two important conclusions can be drawn.
whatever is the atomicity of the gas, the difference remains the same.
(ii) for monoatomic gases, the ratio of two heat capacities (γ) is the same i.e., 1.666.
[wp_ad_camp_1]
Polyatomic gases:
the gases which contain two or more atoms in their molecules have higher values of Cp and Cv from those of monoatomic gases. the reason is that monoatomic gases only need translational energies while polyatomic gases spend their energies for rotational and vibrational motion as well. so for polyatomic gases,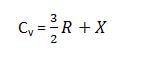
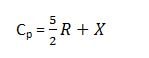
‘X’ is the contribution of energy for rotational and vibrational motions.
two important conclusions are,
the table gives us the Cp, Cv and γ values for various gases.
[wp_ad_camp_3]
the heat capacity of gases at 25°C (JK-1 mol-1)
| Gases | Cp | Cv | Cp – Cv | γ |
| Argon | 20.84 | 12.49 | 8.31 | 1.66 |
| Helium | 20.79 | 12.48 | 8.31 | 1.66 |
| Mercury vapors | 20.66 | 12.38 | 8.28 | 1.66 |
| Iodine vapor | 20.80 | 12.48 | 8.32 | 1.67 |
| Chlorine | 33.84 | 25.03 | 8.81 | 1.35 |
| Hydrogen | 28.80 | 20.52 | 8.28 | 1.41 |
| Hydrogen chloride | 29.12 | 20.82 | 8.30 | 1.41 |
| Nitrogen | 29.10 | 20.81 | 8.29 | 1.40 |
| Oxygen | 29.40 | 21.05 | 8.35 | 1.40 |
| Carbon dioxide | 37.10 | 28.81 | 8.29 | 1.30 |
| Hydrogen sulfide | 33.10 | 24.75 | 8.35 | 1.33 |
| Nitrous oxide | 32.58 | 25.26 | 8.32 | 1.32 |
| Sulfur dioxide | 38.10 | 29.32 | 8.88 | 1.30 |
still curious? watch this video:
Some common questions about heat capacities of various substances are given that people ask on the internet.
[wp_ad_camp_5]
What is the specific heat of Air?
Specific Heat Capacities of air at 300 K are CP = 1.00 kJ/kg.K, Cv =0.718 kJ/kg.K,, and k = 1.4.
What is the specific heat of Water?
The specific heat of water is 1 calorie/gram °C = 4.186 joule/gram °C which is higher than any other common substance.
What is the specific heat of Aluminium?
The specific heat of Aluminium is 0.902= S (J/g 0C) & 90.2 C (J/0C) for 100 g