Collision Frequency Definition & Formula
How Can we define collision frequency of gas molecules?
What is Collision Frequency?
if we follow a single molecule in one cm3 of the gas and want to observe that, how many collisions are being faced by this molecule in one second, then it will be collision frequency of that molecule.
so, we can say that
collision frequency in chemical kinematics is defined as the number of collisions that takes place per second per unit volume of the reaction mixture between two reactant molecules considered as hard spheres.
( source )
it is denoted by ZI . its value should depend upon the velocity of gas molecules, sizes of molecules and closeness of the molecules in the vessel.
Derivation for the Expression of Collision Frequency (ZI):
consider a molecule ‘A' is traveling in the center of the imaginary cylinder from left to the right. the imaginary cylinder is supposed to be present in the vessel of a gas.
the diameter of this cylinder is 2σ. the diameter of the molecule itself is “σ”. it means that two molecules can travel in this imaginary cylinder simultaneously.
the average velocity of the molecule traveling in the center of the cylinder is ̅C ms-1. if the length of the imaginary cylinder is supposed to be is ̅C meters, then it means that the molecule ‘A’ will approach the other end of the cylinder in one second.
the following diagram makes the idea clear.
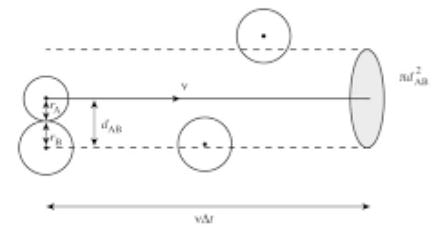
there are many molecules present in this imaginary cylinder. the categories of molecules are ‘B’, ‘C’, ‘D’ and ‘E’.
the molecule ‘A’ can collide with ‘B’ type molecules doing head-on collisions, with ‘C’ type, right-angled collisions with ‘D’ grazing collision and there will be no collision with molecules of the type’E’. keep it in mind, that there are many molecules of each category in this cylinder.
Now! the question arises, that how many collisions this molecule ‘A’ will face while moving from one end of the cylinder to the other.
its answer is that the number of collisions depends upon the number of molecules in this imaginary cylinder.
How to count the number of molecules?
it’s very easy.
Let the radius of the imaginary cylinder is = σ
The base area of this imaginary cylinder = πσ2
Length of the cylinder in meters = ̅C
The volume of the imaginary cylinder = π πσ2 ̅C
Let the number of molecules in one cm 3 = n
Number of molecules in imaginary cylinder = πσ2 ̅Cn
so, the number of collisions which the molecule ‘A’ will experience in one second
should be = πσ2 ̅Cn.
Be careful, that the number of right-angled collisions is much greater than grazing collisions and head-on collisions. so, the exact number of such collisions should be equal to
we have multiplied by √2 because the relative speed of two molecules approaching each other to do right-angled collision, is √2 ̅C and not ̅C. it means that considering the right-angled collisions, the length of the imaginary cylinder is proposed to be √2 ̅C.
this is the collision frequency of the molecule.