Atomic Size of Elements with Examples & Trends
An atom does not have a definite size, because the statistical distribution of electrons does not abruptly end but merely decreases to very small values as the distance from the nucleus increases. Consequently, the atomic size must be defined in a somewhat arbitrary manner, so various measures of atomic size exist. Measuring an atom, however, is not without problems. Good experimental methods exist.
For example, for measuring the center – to – the center distance between atoms in a molecule. The point is that the effective radius of an atom depends on how it is bonded. The contribution an atom makes to the total bond length depends on the nature of the bond which in turn depends in part on the properties of the other atom. It is possible to assemble a set of approximate atomic radii derived from interatomic—distance measurements.
These are made on various compounds chosen so that each of the atoms is involved in the same kind of bonding. The atomic size is expressed in terms of atomic radii, covalent radii, and van der Waal’s radii.
Atomic Radius to measure Atomic Size
The atomic size is somewhat difficult to define since an atom has no precise outer boundary and no limit beyond which its electron cloud surrounding the nucleus vanishes due to the wave nature of the electron. Additionally, we cannot isolate an individual atom and measure its diameter. We can, however, define an Atom’s size as being of the most probable distance from the nucleus to the outer shell electrons.
Since atoms are generally observed not in isolation, but in contact with other atoms either of the same or of a different kind; thus the atomic size depends to a considerable extent on its environment.
Good experimental methods exist, for measuring, the center to center distance between adjacent atoms in a molecule. Thus “half the distance between the centers of adjacent (bonded or touching) atoms is termed as atomic radius “The point is that the effective radius of an atom depends on how it is bonded.
How to find the Atomic Radius?
The unit that has long been used to describe atomic dimensions is the angstrom unit, A°. However, the angstrom is not a recognized unit, it is still preferred by most scientists who study atomic and molecular dimensions. Appropriate SI units are either the nanometers (nm) or the Pico meter (pm).
1A° = 1 x 1010m = 1 x 108cm = O. 10 nm = 100pm
The atomic radii of elements vary periodica1I throughout the periodic table.
(i) Variation of atomic radii within a group of the Periodic Table
The distance of an electron from the nucleus of an atom primarily depends on the principal quantum number, n, which represents the number of shells.
On moving down a group in a periodic table, atomic radii increase with increasing atomic number, because electrons are added to larger orbitals in higher energy shells which are, on average, farther from the nucleus. This effect decreases the electrostatic attraction between the nucleus and the valence-shell electrons and this decreased electrostatic attraction increases the atomic radii.
The percent increase in atomic radius from one period to the next is large for the elements of lower atomic numbers (e.g., from Li to Na to Kin group LA), but the percent increase in atomic radius is much smaller for the elements of higher atomic number (e.g., from K to Rb to Cs).
In K, Rb, and Cs elements the outer-shell electrons are held more strongly by the nucleus that would otherwise be expected. This is because inner-shell electrons in d and f subshells are less effective than s and p electrons in screening outer-shell electrons from the nucleus. Nevertheless, as a useful generalization, we can say that the more electronic shells in an atom, the larger the atomic radius.
Atomic radii of the alkali metals (Group IA)
| Atom | Nuclear charge | Atomic Radius, nm |
| Li | 3+ | 0.152 |
| Na | 11+ | 0.186 |
| K | 19+ | 0.231 |
| Rb | 37+ | 0.244 |
| Cs | 55+ | 0.262 |
(ii) Variation of Atomic Radii of Elements within a Period
There is a decrease in atomic radii of the representative elements from left to right across a period in the periodic table as electrons are added to the orbitals of the same principal energy level (shell). But with the addition of each electron, the nuclear charge (i.e., atomic number) increases by one.
The increased nuclear charge draws the electron cloud closer and closer to the nucleus and thus decreases the atomic radii of the atoms. The greatest decrease is observed in the second and third periods, which include no transition elements.
The Atomic Radii of Second and Third Period
| Atom | nuclear charge | Radius, nm | Atom | nuclear charge | Radius, nm |
| Li | 3+ | 0.152 | Na | 11+
| 0.186 |
| Be | 4+
| 0.118 | Mg | 12+
| 0.160 |
| B | 5+
| 0.088 | M | 13+
| 0.143 |
| C | 6+
| 0.077 | Si | 14+
| 0.117 |
| N | 7+
| 0.070 | P | 15+
| 0.110 |
| o | 8+
| 0.066 | s | 16+
| 0.104 |
| F | 9+
| 0.064 | Cl | 17+
| 0.099 |
| Ne | 10+
| 0.070 | Ar | 18+
| 0.094 |
We have already stated, the radius of an atom depends on the environment in which it is found. For bonded atoms, we generally speak of a covalent radius, ionic radius, and in case of metals, a metallic radius. For atoms that are not bonded together, the radius is known as van der Waals radius.
(a) Covalent Radius for measuring Atomic Size
The covalent radius of an atom is taken as one half the distance between the nuclei of two identical atoms bonded together by a single covalent bond.
The covalent radii are essentially the single bond covalent radii. Thus we can say that the bond distance between the two atoms A-B should be the arithmetic mean of the bond lengths A-A arid B-B. For example, the C-C bond distance is 0.154 nm and the covalent radius of C-C is d.154/2 = 0.077 nm. Similarly, the covalent radius of Si-Si corners to be 0 118 nm.
Thus, we expect the bond distance between carbon and Si would be a bond length of 0.195 nm, which is in very good agreement with the experimental determined C-Si distance of 0.193 nm in carborundum (silicon carbide. This rule works in simple diatomic molecules but this is not generally the case. In the majority of cases. However, the bond distance between unlike atoms is not equal to the sum of the bond radii of the two bonded atoms.
The deviations can be attributed to many factors like multiple bonds, ionic character, and various possible hybridized orbitals that determine the geometry of the covalently bonded molecules. It may be noted that as the difference between the electronegativities of the two bonded atoms increases, a departure from additively of covalent bond radii becomes more and more marked.
The stronger a chemical bond, the shorter the bond distance. The covalent radii are usually classified as either normal radii, tetrahedral radii, octahedral radii, or square radii depending on the geometry of covalently bonded molecules.
Comparison of atomic radii and single bond covalent radii (in nm)
| Metals | Atomic radius | Single bond covalent radius | Non-metals | Atomic radius | Single bond covalent radius |
| K | 0.231 | 0.202 | C | 0.077 | 0.77 |
| Ba | 0.217 | 0.198 | P | 0.110 | 0.110 |
| La | 0.188 | 0.169 | S | 0.104 | 0.104 |
| Zr | 0.157 | 0.145 | Br | 0.114 | 0.114 |
| Pd | 0.138 | 0.128 | |||
| In | 0.162 | 0.150 |
In the above table, the discrepancies in the values of radii are due to the difference in the electronegativities between the bonded atoms.
Ionic Radii for measuring Atomic Size
When neutral atoms gain or lose electrons completely, ions are formed. The ionic radius is the radius of a spherical ion. Ionic radius may be defined as the distance between the nucleus of an ion and the point up to which the nucleus has an influence on its cloud Comparison of the experimentally measured sizes of the atoms and their principal quantum number, n, which represents the number of shells.
On moving down a group in a periodic table, atomic radii increase with increasing atomic number, because electrons are added to larger orbitals in higher energy shells which are, on average, farther from the nucleus. This effect decreases the electrostatic attraction between the nucleus and the valence-shell electrons and this decreased electrostatic attraction increases the atomic radii.
The percent increase in atomic radius from one period to the next is large for the elements of lower atomic numbers (e.g., from Li to Na to K, in group IA), but the percent increase in atomic radius is much smaller for the elements of higher atomic number (e.g., from K to Rb to Cs). In K, Rb, and Cs elements the outer-shell electrons are held more strongly by the nucleus that would otherwise be expected.
This is because inner-shell electrons in d and f subshells are less effective than s and p electrons in screening outer-shell electrons from the nucleus. Nevertheless, as a useful generalization, we can say that the more electronic shells in an atom, the larger the atomic radius. common stable ions lead us to the following generalizations:
- Positive ions (cations) are always smaller than the neutral atoms from which they are formed.
- Negative ions (anions) are always larger than the neutral atoms from which they are formed.
These generalizations are true for all monoatomic ions. The size of the neutral atom is determined by the attraction of the positively charged nucleus for the outermost electrons, which is in the highest principal energy shell level.
When an atom loses electron/s to form a cation, usually the electrons are lost from the shell of the highest principal quantum number, and the resulting cation has one shell-less than the parent atom. The nuclear charge draws the remaining electrons much closer to itself, so a positive ion is much smaller than the parent atom.
Size of Isoelectronic species
Isoelectronic species are those which have the same electronic configurations (i.e., the same number of electrons) but different nuclear charges. The ions formed by the Group IIA elements (Be2+, Mg2+, Ca2+, Sr2+, Ba2+ are significantly smaller than the isoelectronic ions formed by the group IA elements in the same period.
For example, Be2 (r = 0.03 1 nm) is much sma1lerthan Li( r = O.O6Onm)., Both ions have 1s2 electronic configuration. A beryllium ion, Be2, is formed when a beryllium atom loses two electrons while the 4+ nuclear charge remains constant.
The 4+ nuclear charge in Be2 ion draws the remaining two electrons much closer to itself than the 3+ nuclear charge of Li-ion can draw two electrons to itself. Therefore, Be2 is much smaller than Li-ion. Similarly Mg2- ion is smaller than Na ion.
Similar reasoning leads us to conclude that the ions formed by the Group IIA metals (Al3+, Ga3+, ln3+, Tl3+) should be even smaller than isoelectronic ions formed by Group IA and Group IIA formed in the same period. In summary, as the magnitude of the positive charge on isoelectronic ions increases, their size decreases.
If an element exhibits more than one positive valence, then the radius decreased progressively with the loss of electrons as shown in table 1.7.
The Decrease in the Atomic Size in producing various Cations
| Atom Atomic radius, nm | Fe 0.126 | Mn 0.129 | Pb 0.175 |
| Ion Ionic radius, nm | Fe 2+ 0.126 | Mn 2+ 0.129 | Pb+2 0.175 |
| Ion Ionic radius, nm | Fe 3+ 0.060 | Mn 4+ 0.052 | Pb+4 0.84 |
When an atom gains one or more electrons to form a negative ion, the nuclear charge of the atom remains constant, but increased electron-electron repulsion causes the effective volume of the electron cloud to expand greatly, and thus. the size of the anion increases. The greater the magnitude of the negative charge on the isoelectronic ion, the larger the size of the ion. Thus oxide ion, 02- is larger than the isoelectronic fluoride ion F-.
As a final illustration of ionic sizes, let us predict the trend in sizes of the isoelectronic species S2-, Cl-, Ar, K+, Ca2+. These five species all have the electronic configuration 1s22s22p63s23p6. Because all five species have the same electronic configuration, there is no difference in shielding due to inner electrons.
The five do differ, however, in the nuclear charge that acts to attract the 18 electrons. The nuclear charges of all these species are; Ca2+ = 20+ ; K = 19+ ; Ar=18+, CF 17+; S2- =16. The larger the nuclear charge, the greater will be the force of attraction, on the energy level of electrons, and thus smaller in size. This order is Ca2 < K <Ar < CF <S2 (smallest to largest).
Example
The following species are isoelectronic with the noble gas neon. Arrange them in order of increasing size and comments on ‘the principals involved in doing so, Ne, Na+, F-. 02-, Mg2+.
Solution
All the five species have in common the electronic configuration. Is2 2s2 2p6.
The greater the ‘nuclear charge, the more strongly the electrons are held and the smaller the species. Mg2+ has the greatest nuclear charge, 12+, thus Mg2+ is the smallest followed by Na+. If a species has an excess of electrons over protons, it becomes larger than the corresponding noble gas atom, the greater the nuclear charge the larger the size. Thus O2- is the largest species. The order is Mg2+ < Na+ <Ne< F- <02-.
Metallic Radius (The Crystal Radius)
It is used for metal atoms which are assumed to be closely packed spheres in the metallic crystal. The metal atoms are supposed to touch one another in the crystals.
The metallic radius is defined as one-half of the distance between the nuclei of two adjacent metal atoms in the metallic close-packed crystal lattice. The metallic radius is about 10 to 15 % higher than the single bond çovalent radii. The metallic radii are smaller than the van der. Waals radii, since the bonding forces in the metallic crystal lattice are much stronger than the van der Waals forces. The metallic (atomic) radius of Na metal is 0. 186nm.
Van der Waals Radiiand Atomic Size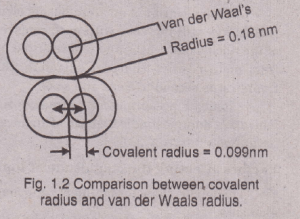
The non-metallic elements in the solid-state usually exist as aggregations of molecules. The bonding within a non-metal molecule is largely covalent in character, and yet individual molecules are held to each other by weak forces called van der Waals forces, “Half of the internuclear distance between two non-bonded atoms within two adjacent molecules is called van der Waals radius.
The radii of this type are non-bonded. These forces are absent when we have substance in a gaseous condition but are present in a crystal lattice at low temperatures. The van der Waals radii are much larger than covalent radii, e. g., the ionic radius of Br- ion is 0.125 nm, the covalent radius of Br is 0.114nm and the van der Waals radius of Br is 0.196 nm.
Noble gases do not form covalent bonds. Thus in crystals of noble gases, no chemical forces operate between the atoms. .It is only the van der Waal’s forces that are attractive forces prevailing in these atoms. Thus, for noble gases in the solid-state, the metallic radii (i.e., atomic radii) are actually van der Waals radii.