Difference Between Precision and Accuracy
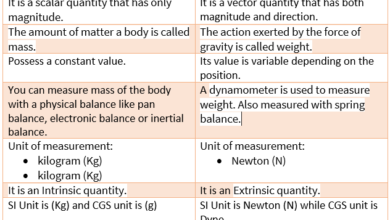
Precision and Accuracy are commonly used as synonyms but actually, they are not. The difference Between Precision and Accuracy is that Precision is the measure of the reproducibility of the measurement, cannot be improved, and is necessary but not a sufficient condition for accuracy while accuracy is conformity to truth, can be improved and is necessary but not sufficient condition for precision.
Explanation
when we measure something, we actually compare two different types of physical quantities. one is regarded as the base quantity which we need to measure e.g. 1kg of sugar, and the other one is considered conventionally adopted standard value.
so, as a result, both the terms precision and accuracy have different meanings and completely independent of each other. their final results will be approximately equal or have some precise value. they can’t be equal to the initial value.
What is Precision?
Precision means how close the measured values are to each other. A precise measurement is one that has less absolute uncertainty. The precision of a measurement is determined by the instrument or device being used
The precision of a measurement depends upon the size of the unit you use to make a measurement.
The smaller the unit, the more precise the measurement. The precision of measurement describes the units you used to measure something.
For example, you might describe your height as “about 6 feet”. That wouldn’t be very precise. If however, you said that you were ’74 inches tall’, that would be more precise.
What is Accuracy?
Accuracy means how close a measured value (result) is to the actual (true) value. The accuracy of a measurement is the difference between your measurement and the accepted correct answer. The bigger the difference, the less accurate your measurement.
An accurate measurement is one that has fewer fractional or percentage errors. the accuracy of a measurement depends on the fractional or percentage uncertainty in that measurement.
Example:
When the object is recorded as 25.5 cm by using a meter rod having the smallest division in millimeter. it is the difference between two readings of the initial and position. The uncertainty in the single reading as discussed before is taken as ±0.05 cm which is now double and called absolute uncertainty equal to ±0.1 cm.
Absolute uncertainty, in effect, is equal to the least count of the measuring instrument. This is called precision:
Case (I):
Precision or absolute uncertainly (least count) = ±0.1 cm
Fractional uncertainty: 0.1 cm⁄ 25.5 cm = 0.004
Percentage uncertainty: 0.1 cm/ 25.5 cm x 100/100 = 0.4/100 =0.4%
case (ii):
Another measurement is taken by vernier calipers with the least count as 0.01 cm is recoded as 0.45 cm. It has Precision or absolute uncertainty (least count) = ±0.01 cm
Fractional uncertainty = 0.01cm/0.45cm = 0.02
= 0.1cm/0.45cm x 100/100 = 2.0%
So the reading 25.5 cm taken by meter rule is although less precise but is more accurate having less percentage uncertainty or error. Whereas the reading 0.45cm taken relative, measurement Which important. The smaller the physical quantity, the more precise instrument should be used.
Here the measurement of 0.45 cm demands that a more precise instrument, such as a micrometer screw gauge, with the least count of 0.001 cm, should have been used.
Assessment of Total Uncertainty in the Final Result
Every measurement has a degree of uncertainty associated with it. The uncertainty derives from the measuring device and from the skill of the person doing the measuring. The total uncertainty in the final result can be found as follows.
in case of addition and subtraction:
for example, the distance ‘x’ found by the difference between two separate position
X1 = 10.5 ± 0.1 cm
and
X2 = 26.8 ± 0.1 cm
the difference x between them is recorded as
x=x2 – x1
= (26.8 ± 0.1) – (10.5 ± 0.1)
= 16.3 ± 0.2 cm
In Case of Multiplication and Division
Percentage uncertainties are added.
for example;
maximum possible uncertainty in the value of resistance R of conductor determined from the measurement of potential difference V and resulting Current flow’I’ by using V= IR is found as follows;
V= 5.2 ± 0.1 V
I= 0.84± 0.05 A
the percentage uncertainty for V = 0.1/5.2 x 100/100 = about 2%
the percentage uncertainty for I = 0.05/0.84 x 100/100 = about 6%
hence total uncertainty in the value of resistance R when V is divided by I is 8%.
the result is thus given as R = 5.2V/ 0.84A = 6.19 V/A
= 6.19 ohms with a percentage uncertainty of 8%.
because percentage uncertainty for V is 2% and for I is 6%. so,
total uncertainty = 2% + 6% = 8%
hence R= 6.02 ± 8% ohms
R= 6.02 ± 0.5 ohms
in the case of power factor
Multiply the percentage uncertainty by that power.
For example,
In the calculation of the volume of a sphere using V=4/3(πr3)
% age uncertainty in V age uncertainty in radius r.
When the uncertainty is multiplied by the power factor, then it increases the precision demand of measurement. If the radius of a small sphere is measured as 2.25cm by a vernier caliper with the least count of 0.01 cm. then the radius r is recorded as
r= 2.25 ± 0.01 cm
Absolute uncertainty in r = Least count = ±0.01cm
%age uncertainty in r =0.01cm/2.25cm x 100/100 =0.4%
Total Percentage uncertainty in V= 3 x 0.4 = 1.2%
this, volume V=4/3(πr3)
= 4/3( 3.14)(2.25)3=47.689cm3 with 1.2 uncertainty
hence the result should be recorded as
V= 47.7 ± 0.6 cm3
In Case Of Average value of Many Measurement
- Find the average value of measured values.
- Find deviation of each measured value from the average value.
- the mean deviation is the uncertainty in the average value.
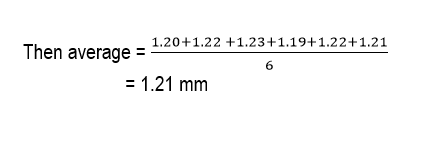
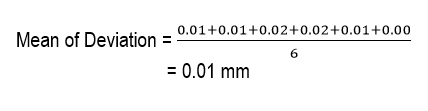
The six readings of the micrometer screw gauge to measure the diameters of a wire in mm are; 120. 1.22, 1.23, I.19, 1.22, 1.21.
The deviation of the readings, which are the differences without regards to the Sign, between each reading and average values are 0.01, 0.01, 0.02. 0.02, 0.01, 0.00.
In the case of the timing experiment
The uncertainty in the time period is found by dividing the least count Of timing measurement instruments by the number of vibrations.
For example,
The time Of 30 vibrations of a simple pendulum recorded by a stopwatch accurately up to one-tenth of a second is 54.65. Thus, the time period is given by
T =54.6/30 =1.82s
Uncertainty in the time period: Least count /no. of vibrations = 0.1s/30 = 0.003s
thus, time period T is written as T= (1.82±0.003)s
You May Also Like: