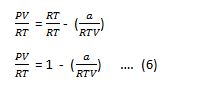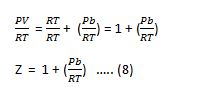Deviation of Gases From Ideal behaviour
What makes a gas ideal?
speaking about the deviation of gases, when we consider the behavior of real and ideal gases, the gases which obey Boyle’s law, Charles’s law, or general gas equation are said to be ideal.
In order to check the ideality of gas, we can plot a graph between PV= NRT =Z, and the pressure of the gas for one mole of gas.
In the case of an ideal gas, a straight line is expected parallel to the pressure axis showing that for one mole of gas the compressibility factor (Z) should be one.
Anyhow, it has been observed that the most common gases like H2, N2, He, CO2, etc. do not follow the straight line as shown in the diagram.
It means that the product of P and V does not remain constant, at a constant temperature.
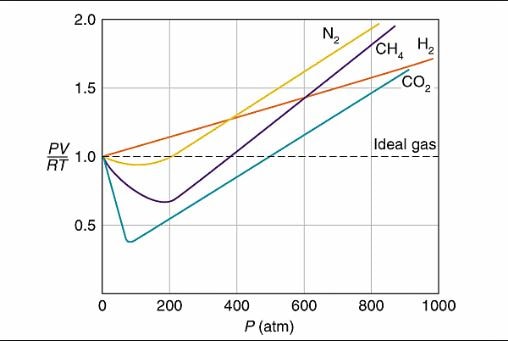
The graph of the gas at 17ᵒC, show more deviations from ideal behavior than at 100ᵒC.
Moreover, the extent of deviation of these gases is more prominent at high pressures. We draw an important conclusion from the above graphs.
- The gases are comparatively ideal at high temperatures and low pressures.
- The gases become non-ideal at low temperatures and high pressures.
watch this video!
Causes for deviation from ideality
Kinetic theory is the foundation stone of all the gas laws and the general gas equation.
There are two faulty assumptions in the kinetic theory of gases for the deviation from the ideal behavior of gases. that can clear the idea about why do gases deviate from ideal behavior.
Let us recall these faulty assumptions and try to find the remedy for them.
- There are no forces of attractions among the molecules of gases.
- The actual volume of gas molecules is negligible as compared to the volume of the vessel.
Both these postulates are correct, at low pressures and high temperatures and these postulates become wrong at low temperatures and high pressures.
Actually, low temperature and high pressure become responsible for the creation of forces of attractions, and moreover, the actual volume doesn’t remain negligible.
It is necessary to account for the actual volume and mutual attractions of molecules.
This job was done by Van der Waal.
Van der Waal’s Equation For Real Gases
Van der Waal modified the general gas equation and performed the corrections i.e., volume correction and pressure correction.
Volume Correction:
Van der Waal thought that some of the volumes of the vessel are occupied by the molecules of the gas and that volume is not available for the free movement of the molecules.
actually, we need the free volume of the gas and that is obtained when we subtract the volume of molecules from the volume of the vessel.
Vfree = V vessel – V molecule
Let ‘V’ free is ‘V’ and ‘V’ molecule is ‘b’ for one mole of a real gas.
So, V = Vvessel – b ……. (1)
This ‘b’ is called the effective volume of gas molecules. Keep it in mind that ‘b’ is not the actual volume of gas molecules, but is roughly equal to 4 times their molar volumes. If we have one mole of a gas, then
b= 4Vm
Vm= actual volume of gas molecules for one mole of the gas.
Pressure correction:
The pressure which is exerted on the walls of the vessel is due to collisions. Since there are forces of attraction,
molecules cannot hit the walls of the vessel with that much force, with which they should have been in the absence of attractive forces.
It means that the pressure is observed on the walls of the vessel is a little bit less than the ideal pressure.
P obsereved = P ideal – P lessened
The pressure which is being lessened is denoted by P’.
P = Pi – P’
Pi = P + P’
The value of P’ given by van der Waal is a/V2.
P’ = a/V2
In order to estimate the volume of P’ which is lessened pressure, we proceed as follows.
Suppose we have two types of molecules A and B. let the concentrations of A and B type molecules are CA and CB. the force of attraction between A and B is proportional to CA and CB. so,
P’ ∝ CACB
Now suppose that “n” is the number of moles of A and B separately. Hence n/V is the number of moles dm-3 of A and B separately. “V” is the volume of the vessel containing the gas.so,
P’ ∝ n/V. n/V
or P’ ∝ n2/V2
or P’ = an2/V2
Where a = constant of proportionality
If the number of moles of gas is unity, then n= 1
P’ = a/V2
Pressure of the ideal gas Pi = P = a/V2
So, Pi = P + a/V2 ….. (2)
“a” is the coefficient of attraction. In other words, it is attraction per unit volume and is a constant for a particular real gas.
Introducing these corrections, the general gas equation is modified.
[wp_ad_camp_4]
(P + ) (V – b) = RT …. (3)
For ‘n’ moles of a gas,
(P + ) (V- nb) = nRT …. (4)
‘a’ and ‘b’ are called van der Waal constants.
you can understand Van Der Waal’s Equation concept by video!
Nature of the van der Waal constants:
These constants ‘a’ and ‘b’ are the quantitative measurement of non- ideality of the gases.
They are usually determined experimentally by measuring the deviation from the real gas equation, under suitable conditions of temperature and pressure i.e., those conditions when the effects of molecular volume and mutual attractions predominate.
The values of ‘a’ and ‘b’, depending upon the nature of the gas and the units of volume and temperature.
Units of ‘a’ and ‘b’:
The units of van der Waal’s constants are derived as follows:
Since, P’ = an2/V2
a = P’V2/n2 = atm(dm3)2/mol2 = dm6 atm mol-2
in S.I. units
a= P’V2/n2 = Nm-2 x (m3)2 / mol2 = Nm4/ mol-2 = Nm4 mol-2
‘b’ has the units of volume mol-1 so, it may be expressed as dm3 mol-1 or m3mol-1.
Gases | a Dm6 – atm mol-2 | a Nm4 mol-2 | b dm3 mol-1 | b m3 mol-1 |
| H2 | 0.244 | 24.72 x 10-2 | 0.02661 | 26.61 x 10 -6 |
| He | 0.034 | 34.5 x 10-3 | 0.02370 | 23.70 x 10 -6 |
| O2 | 1.360 | 138 x 10-2 | 0.03180 | 31.80 x 10 -6 |
| N2 | 1.390 | 141 x 10-2 | 0.0913 | 39.13 x 10 -6 |
| CO2 | 3.592 | 346 x 10-2 | 0.04267 | 42.67 x 10 -6 |
| NH3 | 2.250 | 422 x 10-2 | 0.03710 | 37.10 x 10 -6 |
| CH4 | 2.250 | 228 x 10-2 | 0.04280 | 42.80 x 10 -6 |
Interconversion of units:
dm3 mol-1 = 10-3 m3mol-1
dm6 atm mol-2 = 10-6m6 x 101325 Nm-2 mol-2
= 1.01325 x 10-1 Nm4 mol -2
Van der Waal’s constants for some important gases:
Since H2 and He are non-polar gases so, their ‘a’ factors are sufficiently smaller than many other gases. CO2 and NH3 are big sized molecules and so their ‘a’ factors are sufficiently high.
‘b’ factor is the measurement of the volume of gas molecules in the closest possible positions of molecules.
This factor is also sufficient for CO2, NH3, and CH4.
When we say that, the value of the ‘b’ factor H2 is 0.02661 dm3 mol-1, then it means that it is 26.61 cm3 mol-1.
In other words, we can say that one mole of H2, i.e., 2.061 grams will occupy a volume of 26.61 cm3 when the molecules are so close to each other in the gaseous state.
It means that the calculated volume of H2 gas molecules is 26.61 cm3.
The validity of van der Waal’s Equation:
While we have discussed the non-polar behavior of gases by graphical explanation, it was noticed that some of the gases have lower values of PV/RT=Z, then expectations at low pressures.
At high pressures, the value of PV/RT=Z increases too much.
We have to justify these trends of gases.
For this purpose, we change the shape of Van der Waal’s Equation.
(P+ a/V2)(V-b) = RT
PV – Pb + a/v – ab/V2 = RT
PV = RT + Pb – a/V + ab/V2 …. (5)
At low pressure:
When the pressure is smaller than the volume will be larger, hence, the term ‘Pb’ and ab/V2 in equation (5) may be neglected in composition to a/V represents the effect of attractions between the molecules.
PV = RT – a/V
Divide the Equation by ‘RT’ into both sides
owing to the fact, PV/RT is also called the compressibility factor and Is denoted by Z.
Hence Z = 1 – a/RTV ….. (7)
It means, at low pressures the compressibility factor is less than unity. It explains that the graphs of N2 and CO2 lie below the ideal curve.
When we increase the pressure, ’V’ decreases, and the value of ‘Z’ increases. It means that the curve should show an upward trend.
At high pressure:
at high pressure the volume ‘V’ is small.
In this case,
we will ignore both terms a/V and ab/V2 .now the Equation (5) has changed to the following equation,
PV = RT + Pb
Dividing the Equation with ‘RT’ into both sides,
It means that the high pressure ‘Z’ is greater than 1 and so the graph between ‘Z’ and ‘P’ lies above the ideal gas curve. When we apply the increment of pressure, the factor Pb/RT increases further and ‘Z’ becomes greater and greater.
At extremely low pressure:
At extremely low pressure, we say that the pressure approaches zero. In this way, ‘V’ becomes very large.
Under these circumstances, the term Pb, a/V and ab/V2 will become negligible and can be ignored relative to ‘RT’.
Thus, equation (5) is converted to the following:
PV = RT
It means that at extremely low pressures, the real gases behave ideally.
At high pressure:
It means that at high temperatures, the real gases behave ideally.
Exceptional behavior of H2 and He:
the molecules of H2 and He have a very small size and they are non-polar in nature. They have the least attractive forces. Their ‘a’ factor is very small.
for this reason, a/V and ab/V2 in equation (5) can be ignored. Hence, we can write equation (5) as follows:
PV = RT + Pb
Dividing by ‘RT’
PV/RT = 1 + Pb/RT
Z = 1 + Pb/RT ( PV/RT = Z )
from the above results,
It means ‘Z’ is always greater than 1. as a consequence, Graphs for H2 and He also shows that the curves for hydrogen lie above the ideal curve.