First Law of Thermodynamics statement & derivation
Statement of First Law of Thermodynamics
The first law of thermodynamics also known as the ‘Law of Conservation of Energy’.
[wp_ad_camp_1]
“ Energy can neither be created nor destroyed, but only be changed from one form to another form”.
Or
“ The total energy of a system and its surrounding remain constant”.
Mathematical Form and derivation
Consider a system whose initial system is ‘E1’ let a quantity of heat ‘q’ absorbed by the system from the surroundings and does some work ‘W’ on the surroundings while the internal energy change to
‘E2’.
Then, change in internal energy is given by
ΔE = E1 – E2
According to the first law of Thermodynamics
ΔE = q – W
Value of ΔE is negative when the system loses energy and positive when system gains energy.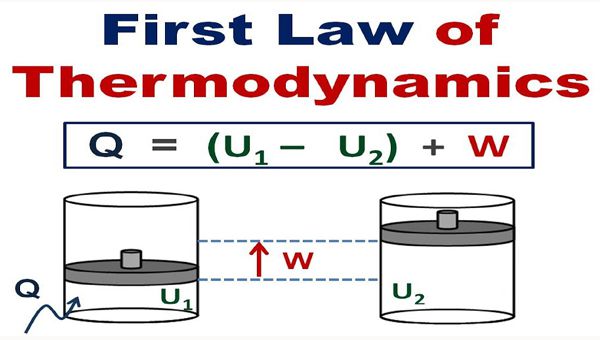
Pressure-Volume Work
Consider a gas enclosed in a cylinder, fitted with a frictionless and weightless piston. Let the area of the piston is ‘A’ external pressure acting on the piston ‘P’, the force exerted by the gas on the piston ‘F’.
[wp_ad_camp_2]
Now, if the system expands, and the piston moves against the surroundings travelling a distance ‘ΔI’. Then,
Work = Force x Displacement
W = F x ΔI ———– 1
Since,
P = F/A
Therefore,
F = P x A ———— 2
Put the value of ‘f’ into equation # 1, we get
W = P x A x ΔI ———— 3
Since,
A x ΔL = ΔV
So, equation # 3 we can write as
W = P x ΔV
Or
W = P ΔV
According to the first law of thermodynamics
ΔE = q – w ———– 4
Put the value of ‘W’ in equation # 4 we get
ΔE = q – P ΔV
Or
q = ΔE + p Δ V
[wp_ad_camp_3]
Application of First Law of Thermodynamics
Process At Constant Volume
According to the first law of thermodynamics
ΔE = q – P Δ V
ΔE = q v – P Δ V ————– 1
Where, qv = heat absorbed at constant volume when the volume of the system not change
Δ V = 0
Under this condition, no work is done
P Δ V = p x 0 = 0
Hence, equation # 1 becomes
Δ E = q v ————- 2
This equation shows that at constant volume, the heat evolved is equal to the change in the internal energy and no work is done.
Process At Constant Pressure
When heat is given to system at constant pressure the internal energy of the system increases, as a result of which the system performs work on the surroundings:
[wp_ad_camp_4]
Thus,
qp = ΔE + PΔV ———- 1
where qp is the heat absorbed at the constant pressure
we know that
ΔE = E1 – E2
ΔV = V1 – V2
Then equation # 1 can be written as:
= (E2 – E1) + P(V2 – V1)
qp = (E2 + PV2) – (E1 + PV1) ———- 2
the enthalpy ‘H’ is mathematically defined as:
H = E + PV
At initial state
H1 = E1 + PV1
At final state
H2 = E2 + PV2
Substituting the value in equation # 2 we get
qp = H2 – H1 = Δ H
qp = ΔH ———– 3
Equation #1 can be written as:
ΔH = Δe + PΔV ———- 4
Equation #3 shows that heat absorbed or evolved from a system at constant pressure is equal to the change in enthalpy of the system.
Thus, change in enthalpy is the heat absorbed or evolved by a system at constant pressure.