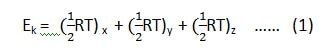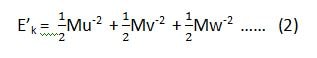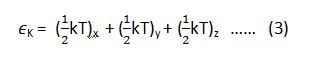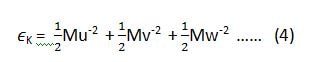In physical chemistry, for a monoatomic gas, the translational energy associated with one mole of the molecule at any temperature is 3/2RT.
According to the law of equipartition of energy, 1/2RT is expended along the x-axis, 1/2RT along the y-axis and 1/2 RT along the z-axis.
we have already considered that if the component velocities are u, v and w, then the kinetic energies along x, y and z-axis are,
U– , V– and W– are the average velocities along x, y, and z-axis.
if we want to apply this law on the equipartition of energy for a single molecule, then equation (1) and (2) can be written as (3) and (4) respectively.
where ‘K’ is Boltzmann constant.